Intérêts, inflation, mais quel est le lien?

Souvent, les deux phénomènes sont expliqués distinctement. Dommage. Ici, tout est réconcilié. A vous lire 😉

Définition de l’intérêt

L’intérêt est la rémunération due au créancier au titre de sa créance.

L’intérêt, c’est la rémunération de celui qui prête de l’argent.

Quand vous placez de l’argent sur un compte d’épargne, en fait, c’est comme si vous prêtiez de l’argent à votre banque. En échange, elle vous rémunère par de l’intérêt. Enfin, elle devrait. Parce qu’aujourd’hui … 🙄

De même, quand vous demandez à la banque de l’argent à prêter, vous faites alors un crédit, il est logique de rémunérer la banque et de lui verser des intérêts.

Les intérêts, comment ça fonctionne?

On distingue deux modes de calcul de l’intérêt.

Dans le mode des intérêts simples, les intérêts sont versés à chaque échéance. Dans le mode des intérêts composés, les intérêts restent avec le principal et le font gonfler.

Les intérêts simples

Si l’on prend l’exemple d’un placement de 1.000€ sur une durée de 5 ans au taux d’intérêt annuel de 3%, le calcul se fait comme ceci:

Après 1 an, vous touchez 1.000€ x 3% = 30€

Après 2 ans, vous touchez 1.000€ x 3% = 30€

Après 3 ans, vous touchez 1.000€ x 3% = 30€

Après 4 ans, vous touchez 1.000€ x 3% = 30€

Après 5 ans, vous touchez 1.000€ x 3% = 30€ , plus le capital que vous avez prêté: 1.000€

Au final, votre placement de 1.000€ sur 5 ans au taux de 3% vous rapportera : 5×30€ = 150€

Les intérêts composés

Si l’on reprend le même exemple d’un placement de 1.000€ sur une durée de 5 ans au taux annuel de 3%, le calcul se fait comme ceci:

Après 1 an, votre placement rapporte 30€, mais vous ne touchez rien. Les 30€ s’ajoutent au capital.

Après 2 ans, votre placement rapporte 1.030€ x 3% = 30,90€, qui viennent s’ajouter au capital.

Après 3 ans, votre placement rapporte 1.060,90€ x 3% = 31,827€, qui viennent s’ajouter au capital.

Après 4 ans, votre placement rapporte 1.092,727€ x 3% = 32,78181€, qui viennent s’ajouter au capital.

Après 5 ans, votre placement rapporte 1.125,50881€ x 3% = 33,7652643€, qui viennent s’ajouter au capital.

Au final, votre placement de 1.000€ sur 5 ans au taux de 3% vous rapportera : 1.000€ x (1,03)^5 – 1.000€ = 159,27€

Les intérêts en images

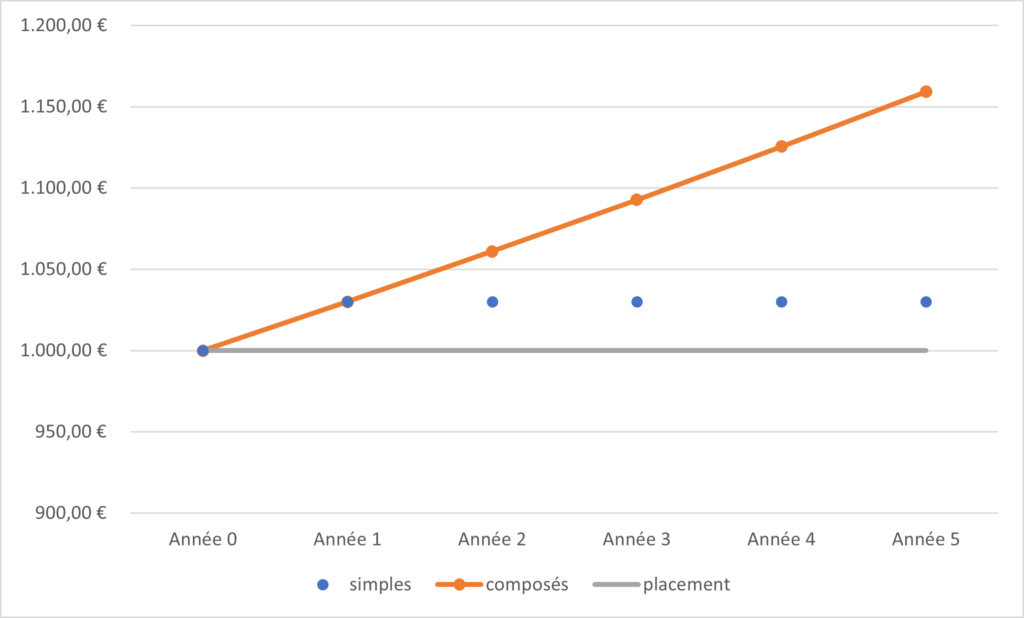
Les intérêts en formules

Pour calculer les intérêts, on a besoin de trois éléments:

C, le capital (appelé aussi le principal)
i, le taux d’intérêt
t, le temps de placement

Attention ! Piège ! Il faut que le taux d’intérêt concorde avec le temps de placement. Si l’on parle d’un placement sur 5 ans, le taux doit être annuel. Si l’on parle d’un placement en mois, le taux doit être mensuel. Je vous explique plus loin comment transformer les taux annuel en mensuel et vice-versa.

A la fin du placement, vous obtiendrez donc :

Les intérêts simples: C + [C x i x t]

Les intérêts composés: C x (1+i)^t

Pour trouver le rendement, c’est-à-dire ce que vous touchez EN PLUS du capital que vous placez, il suffit d’enlever le principal à la formule précédente.

On a donc:

Le rendement avec les intérêts simples: [C x i x t]

Le rendement avec les intérêts composés: [C x (1+i)^t] -C

Un exemple pour illustrer

Capital: 10.000€

Taux d’intérêt annuel: 5%

Durée du placement: 10 ans

Calculez les rendements pour chacun des modes de calcul des intérêts.

	Intérêts simples	Intérêts composés
Ce que l’on obtient au final	10.000 x 5% x 10 + 10.000 = 15.000 €	10.000 x (1,05)¹⁰ = 16.288,95€
Rendement du placement	5.000€	6.288,95€

Dans la réalité, ça veut donc dire que dans le cas d’un investissement avec des intérêts simples, l’investisseur a touché chaque année 500€. C’est super s’il a pu les placer ailleurs, c’est dommage s’il les a dépensés dans des futilités.

Le placement en intérêts simples correspond à un placement dans des actions ou des obligations. Les dividendes sont versés chaque année à l’actionnaire et les intérêts sont versés chaque année à l’obligataire.

Le placement en intérêts composés correspond à un placement sur un compte d’épargne ou une assurance pension par exemple. Chaque année, les intérêts viennent alimenter le principal.

Mais à quoi ça sert ?

On l’a vu, savoir calculer et surtout différencier les modes de calcul des intérêts simples et composés, ça peut servir pour calculer le rendement d’un placement.

Mais ce n’est qu’une toute petite partie !

Voici la réponse de notre copain Albert.

« Les intérêts composés sont la plus grande force dans tout l’univers »
— Albert Einstein

Ca veut aussi dire que si chaque jour, quelle que soit votre discipline, si vous décidez de vous améliorer de 0,1% (=1 pour mille), au bout d’une année, vous augmentez votre performance de 1x(1,001)³⁶⁵ = 1,44. Vous augmentez votre performance de près de 50% !!

Bon, tout ça, c’était pour le côté rigolo.

Il y a un autre point, beaucoup moins drôle pour le coup, qui est aussi impacté par ce phénomène, j’ai nommé …

L’inflation

Et oui, l’inflation, c’est le principe des intérêts cumulés, mais à l’envers !

Chaque année, les prix augmentent (vous êtes surpris ??), c’est le phénomène de l’inflation.

L’inflation est une augmentation généralisée des prix sur une période donnée.

Si chaque année, un bien devient plus cher de 2% par an, si vous l’aviez acheté 5€ il y a 10 ans, en moyenne, il devrait valoir aujourd’hui 5x(1,02)¹⁰ = 6,09€.

Vous trouverez ici l’évolution générale des prix en Belgique actualisée.

Vu qu’en Belgique, nous bénéficions de l’indexation automatique des salaires, cette augmentation passe à peu près inaperçue dans le portefeuille des Belges. Bon, il y en aura toujours pour dire, mais franchement, on n’est pas dans les pires.

Par contre, votre épargne elle, elle souffre dramatiquement de ce phénomène !

En effet, l’inflation est d’environ 2% par an depuis quelques années (parfois un peu plus, parfois un peu moins, mais bon, disons).

Donc, pour gagner de l’argent sur une épargne, votre taux d’intérêt devrait être de … oui … de plus de 2% !

Or, aujourd’hui, les taux sont de l’ordre de … 0,1 % !

Donc, chaque année, l’argent sur un compte d’épargne perd 1,9% de sa valeur !

Cumulé !!!

Au bout de 10 ans, votre compte d’épargne affichera 10.000 x (1,001)¹⁰ = 10.100,45€ (chouette, vous avez gagné 100€)

Mais l’inflation aura fait que le bien que vous vouliez acheter à 10.000€ sera devenu dans le même temps 10.000 x (1,02)¹⁰ = 12.189,84 € !! Voilà une perte nette de 2.089,39€ !! Et encore, ici, on est sur un compte gratuit ! Si vous ajoutez à cette perte les nombreux frais bancaires … 😭

Vous voulez en savoir sur les dégâts de l’inflation sur votre épargne? Voici le site de Wikifin et son calculateur.

Donc, surtout, commencez à épargner, même sur un compte d’épargne qui ne rapporte rien, mais très vite, adoptez une stratégie d’investissement.

Et pour illustrer tout ça, voici un article paru sur la rtbf en ce début du mois de janvier. Ils sont encore très gentils en disant que l’épargne ne rapporte presque plus rien. A la limite du doucereux ! Parce qu’en lisant bien, ils n’osent pas vous le dire, mais les comptes d’épargne perdent littéralement leur valeur. Vous le trouverez par ici.

Nous verrons tout ça dans un prochain article. Non, ça ne parlera pas de crypto, ce n’est pas un sujet qui m’intéresse, mais plutôt d’investissements durables, sociétaux, brefs, plus proches de mes valeurs. N’hésitez pas à vous inscrire pour allez plus loin dans cette aventure.

Pascale